VALOR ABSOLUTO

Recordemos que la definición del valor absoluto surge de nociones geométricas, y se relaciona con los conceptos de longitud y distancia.

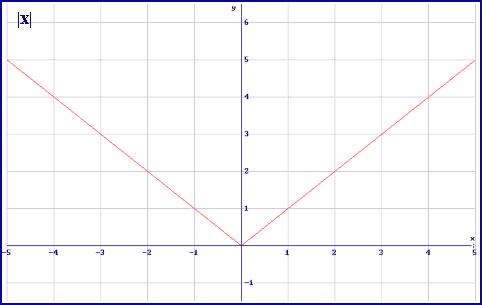
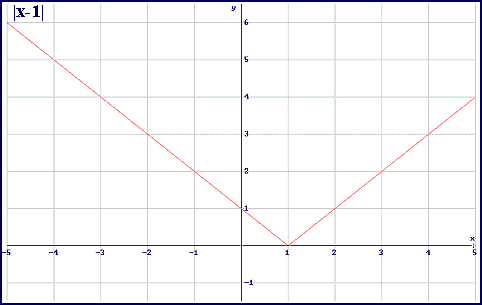
La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula. 

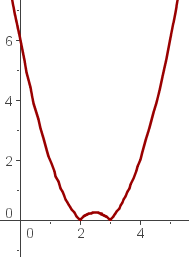
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.

Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:

1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).

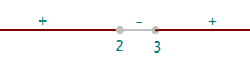
2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada intervalo.

3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.

4. Representamos la función resultante.

Veamos un ejemplo:

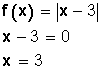
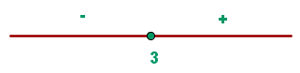
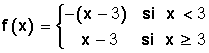
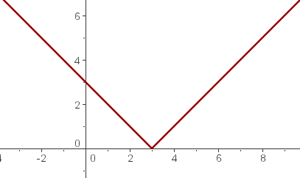
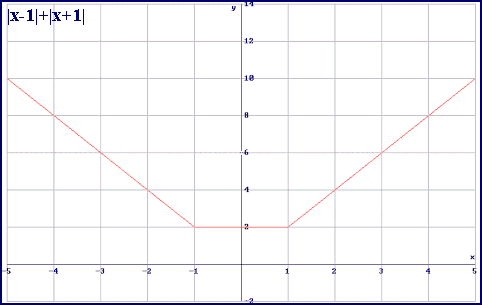
Otro ejemplo:

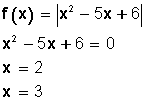
Valor absoluto de un número real

Formalmente, el valor absoluto o módulo de todo número real   está definido por: 2 ejemplos básicos:

Note que, por definición, el valor absoluto de siempre será mayor o igual que cero y nunca negativo. Desde un punto de vista geométrico, el valor absoluto de un número real   es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real

Otras propiedades

Valor absoluto - Parte entera - Parte decimal – Signo

Representa las función valor absoluto:

1) f(x) = |x - 2|

2) f(x) = | x² – 5x + 6|

3)f(x) = |-x² + 5x - 4|

-x² + 5x - 4 =0 x² - 5x + 4 =0 x = 1 x = 4