DOMINIO. ARGUMENTO, IMAGEN Y CONTRADOMINIO

El dominio de una función es el primer conjunto de datos, sus elementos (argumentos)

tienen su imagen en el contradominio.

El argumento es cualquier elemento del dominio.

La imagen es el elemento que le corresponde a un argumento de forma particular.

El contradominio de una función es el segundo conjunto de datos, contiene a

las imágenes.

El rango está conformado por el conjunto de imágenes, algunas veces es igual

al contradominio.

También se puede decir que, una función es una relación en que cualquier elemento

del dominio le corresponde un sólo elemento del codominio, este último

también llamado contradominio.

Una variable representa a aquello que está sujeto a algún tipo de cambio, como

la edad de una persona, la velocidad de un automóvil, el crecimiento de las hojas de

una planta, etc.

Una función expresada como ecuación posee dos variables.

Una de ellas la podemos manipular llamada variable independiente y su consecuencia

llamada variable dependiente. Por ejemplo: y = 2x + 1

Donde, x es la variable independiente, y es la variable dependiente y los números

2 y 1 son constantes.

Existen diversas formas de simbolizar una función, una de ellas es la siguiente:

Función ƒ con dominio en A y contradominio en B,

También podemos representar una función como que se lee “ƒ en x”

En el siguiente ejemplo se muestran los elementos del dominio y codominio de

una función.

En este caso se observa que cada elemento del contradominio es el triple de

cada elemento del dominio, pero disminuido en una unidad, y = 3x - 1

En la notación de una función, ƒ (x) se lee “ imagen de x ”, significa: la imagen del

argumento x bajo la función ƒ .

Por ejemplo, en ƒ (x) = 2x , la regla de correspondencia es que cada elemento en

el rango es igual al doble de cada elemento en el dominio.

Ejemplos:

1. Para

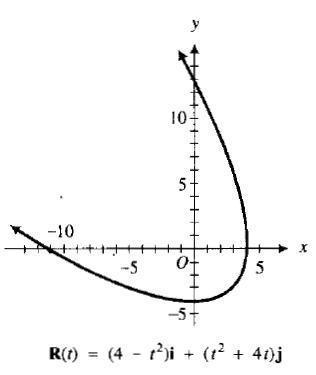
El dominio de una relación o función son todos los valores que puede tomar la variable "x", sin que lafunción se indetermine.
(l conjunto de ida, de partida)
El recorrido o contradominioson los valores que puede tomar la variable "y".
(el conjunto de llegada
La imagen es cada un de los valores que se encuentran en el contradominio ( nótese que el contradominio las incluye a todas,es un conjunto. Imagen se llama a cada una de las que están dentro)

Preimagen (aunque no lo preguntas) son las que se encuentran en el dominio, cada una.

Por ejemplo en la función F: A ----> B
donde la función se define como
F= {(1,a), (7, c), (2, b), (3, a)}

Las imagenes son: a - b - c (son 3, no se vuelve a escribir la repetida)

El Dominio es el conjunto : Dom= {1, 7, 2, 3}

Y el Contradominio el conjunto: Con= {a, b, c}

Dominio y Rango: Gráficas

También podemos representar funciones y relaciones con gráficas. La cantidad independiente normalmente se grafica en el eje horizontal (x) — lo que significa que los puntos en la coordenada x son el dominio. Como la cantidad dependiente normalmente se grafica en el eje vertical (y) , las coordenadas y conforman el rango. Veamos algunas gráficas para entender cómo funciona esto.

Primero, examina la gráfica de puntos discretos. Los únicos valores que conocemos que satisfacen la ecuación son los marcados con puntos. Simplemente leemos las coordenadas x, y los colocamos en un conjunto de valores que representan el dominio. Luego leemos las coordenadas y, y los ponemos en el rango. Para ésta gráfica, el dominio es {-2, 0, 2, 4}. Y el rango es {0, 6, 12, 18}.

Ahora veamos un tipo de gráfica diferente, en el cual la función es una recta continua, que se extiende indefinidamente en ambas direcciones. Esto significa que hay un número infinito de valores que son parte de la función. Para ésta función, no hay restricciones para el dominio ni para el rango. Cualquier número real puede ser una entrada o una salida. Esto significa que todos los números, enteros, fracciones y otros números racionales, incluso números irracionales, son parte del dominio y parte del rango. Como no podemos escribir todas estas posibilidades, simplemente decimos que el dominio y el rango son todos los números reales.

En algunas situaciones sólo uno de los dos, el dominio o el rango, está restringido. Considera la gráfica del valor absoluto de la función, y = |x|. La línea se extiende indefinidamente en ambas direcciones sobre el eje x, por lo que el dominio son todos los números reales. Sin embargo, como el valor absoluto transforma cualquier valor negativo en uno positivo, no existen valores negativos en el rango. El rango está formado de todos los números reales mayores o iguales a 0 — aunque siguen siendo demasiados como para escribirlos todos.

Sumario

Las funciones pueden definirse usando palabras, símbolos, gráficas, tablas o conjuntos de pares ordenados, pero en cada caso las características son las mismas. El dominio es la entrada, el valor independiente — es lo que entra a la función. El rango es la salida, el valor dependiente — es lo que sale de la función. El dominio y el rango pueden estar limitados a unos pocos valores discretos o pueden incluir todos los números reales, hasta el infinito y más allá.

Ejemplo:

F  {(-1,3), (2,4), (-4,-5), (2,6)}

Podemos ver cuatro grupos ordenados de pares,  de los cuales ya dijimos arriba, cuales son D  y cuales son F.

Veamos cómo es un procedimiento de dominio y rango de una funcion:

Y= 2X

Para esto, debemos entonces dar valores a X, de tal modo que cada valor dado a X, nos lleve hallar  un valor de Y.

De este modo.

X   Y

-1- 2

0   0

1   2

Ahora bien, cuando  X vale -1, y vale  -2; cuando X vale 0 , Y vale 0 & cuando  X vale 1 Y vale 2  de este modo, hemos reemplazado valores de a X en el dominio, y valores de Y en el rango, logrando e nuestro ejemplo de dominio y rango de una funcion, un nuevo conjunto de pares ordenados, los cuales son:

(-1-2), (0,0), (1,2)

Cada valor, dominio y rango, pertenece a un punto específico en plano cartesiano, tanto en el eje vertical Y , como en el vertical X, así,  la parábola que representaría ese trazo hallado dados por los pares ordenados, pasara  indefectiblemente por esos puntos, trazando una línea imaginaria.

Este tipo de ejemplos, nos ayudaran para ejercicios posteriores de  este tipo, en los que se pedirá que sobre un plano, se indique el recorrido de una parábola, dadas unas coordenadas o ubicaciones sobre un plano.  El conocimiento y dominio de estos conceptos,  brindara seguridad  y agilidad en el cálculo.