Una
correspondencia unívoca es una correspondencia matemática donde cada elemento
del conjunto dominio se corresponde con solo un elemento del conjunto rango.
Una correspondencia unívoca es una correspondencia matemática donde cada elemento del conjunto dominio se corresponde con solo un elemento del conjunto rango.

Una correspondencia biunívoca es simplemente una correspondencia univoca cuya correspondencia inversa también es unívoca. Es decir: cada elemento del primer conjunto se corresponde con solo un elemento del segundo conjunto, y cada elemento del segundo conjunto se corresponde con solo un elemento del primer conjunto.


Una correspondencia biunívoca es simplemente una correspondencia univoca cuya correspondencia inversa también es unívoca. Es decir: cada elemento del primer conjunto se corresponde con solo un elemento del segundo conjunto, y cada elemento del segundo conjunto se corresponde con solo un elemento del primer conjunto.

Un ejemplo
 |  |
 |  |
Si tenemos una serie de objetos, como los tubos de pintura y los pinceles, y diferenciamos por un lado los tubos y por otro los pinceles, y asociamos a cada tubo con el pincel que tiene el mismo color de pintura, tenemos una relación color de la pintura entre cada tubo y cada pincel que tenga el mismo color.
 |
 |
 |
 |
 |
 |
En este ejemplo, podemos definir un conjunto T de tubos de pintura y otro P de pinceles y asociar a cada tubo del conjunto T, el pincel del conjunto P que tenga su mismo color, esta asociación la representaremos con una flecha del tubo al pincel correspondiente.
Puede darse el caso que tengamos un tubo de un color pero no un pincel con el mismo color de pintura, como en el ejemplo hay un tubo de color rojo pero no hay ningún pincel con pintura de color rojo, por lo tanto del tubo rojo no sale ninguna flecha.
Puede que tengamos un tubo de un color y varios pinceles con pintura de ese mismo color, así en el ejemplo hay un tubo verde y dos pinceles con pintura verde, del tubo de color verde salen dos flechas una hasta cada pincel con pintura verde.
También puede ser que tengamos más de un tubo de un mismo color y un solo pincel con esa pintura, en este caso, como en el ejemplo, de los dos tubos azules salen las dos flechas hasta el único pincel con pintura azul, llegando dos flechas al pincel azul, una de cada uno de los tubos de color azul, como se ve en la figura.
En la figura del ejemplo se ve un pincel con pintura amarilla, pero no hay ningún tubo de pintura amarilla, por tanto a este pincel no llega ninguna flecha.
En resumen la correspondencia mismo color de la pintura entre un conjunto T de tubos de pintura, y otro conjunto P de pinceles, existe en tanto en cuanto al menos un tubo de pintura tiene el mismo color que uno de los pinceles, pudiendo ser esa relación tan sencilla o tan compleja como se quiera.
En una correspondencia matemática los conjuntos no tienen que ser necesariamente numéricos, ni la relación entre sus elementos operaciones aritméticas, sin que por ello deje de ser matemática.
ejemplo 1
| d | (1,d) | (2,d) | (3,d) | (4,d) |
| c | (1,c) | (2,c) | (3,c) | (4,c) |
| b | (1,b) | (2,b) | (3,b) | (4,b) |
| a | (1,a) | (2,a) | (3,a) | (4,a) |
| X×Y | 1 | 2 | 3 | 4 |
en la diagrama anterior, tenemos los conjuntos:
el producto  es:
es:
 es:
es: |  |  | |
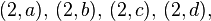 | |||
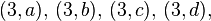 | |||
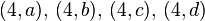 | 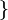 |
el conjunto F es el siguiente:
se puede apreciar que  y que F define la correspondencia en su totalidad.
y que F define la correspondencia en su totalidad.
 y que F define la correspondencia en su totalidad.
y que F define la correspondencia en su totalidad.
ejemplo 2
Partiendo de la correspondencia entre los tubos de pintura T, y los pinceles P, asociando a cada tubo el pincel que tiene pintura del mismo color.
La correspondencia vendrá definida por los pares ordenados:
Vemos que el conjunto inicial es:
y el conjunto final:
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
el producto cartesiano de T por P es el conjunto de pares ordenados de cada uno de los tubos de T con cada uno de los pinceles de P, en la cuadrícula podemos ver en la fila inferior cada uno de los tubos del conjunto T, y en la columna da la izquierda cada uno de los pinceles del conjunto P, donde se cortan una fila y una columna están el tubo y el pincel correspondientes, se ha destacado el fondo de las pares que forman parte de la correspondencia.
Ejemplo
en el diagrama de la figura:
- todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva
- el elemento d de Y, no tiene ningún origen por lo que esta aplicación no es sobreyectiva.
- Segundo ejemplo
Partiendo del conjunto de pinceles con pintura de colores:
Sobre el conjunto de caras pintadas:
Asociando cada pincel con la cara correspondiente:
Dado que cada pincel tiene una cara y solo una cara de su color esta correspondencia es una aplicación, como las caras que tiene pincel de su color, tienen un solo pincel de su color, la aplicación es inyectiva, y como la cara pintada de amarillo, no tiene ningún pincel de este color, la aplicación no es sobreyectiva.
en el diagrama de la figura:
- todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva
- todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.
Si tomaremos por conjunto inicial el conjunto de los números naturales:
y por conjunto final el de los números naturales pares:
Podemos ver que la relación
Por el que a cada número natural x de X, le asociamos un número par 2x de Y, se cumple:
- f: es una aplicación, dado que a cada uno de los valores x de X le corresponde un único valor 2x de Y.
- esta aplicación es inyectiva dado que a cada número par 2x de Y le corresponde un único valor x de X.
- y es sobreyectiva porque todos los números pares tienen un origen
Esto nos permite afirmar que hay el mismo número de números naturales que de números naturales pares, se da la paradoja de que los números naturales pares en un subconjunto propio de los números naturales, esta circunstancia solo se da con los conjuntos infinitos.
Segundo ejemplo
Tomando el conjunto de pinceles como conjunto inicial:
y el de caras como conjunto final:
La correspondencia que asocia cada pincel con la cara de su mismo color es una aplicación porque todos los pinceles tienen una cara con su color y solo una cara de ese color, la aplicación es inyectiva porque un pincel corresponde con una sola cara, y es sobreyectiva porque todas las caras tiene un pincel de su color, al ser inyectiva y sobreyectiva simultáneamente esta aplicación es biyectiva.
Una aplicación biyectiva hace corresponder los elementos del conjunto inicial con los del conjunto final uno a uno, pudiéndose decir que hay el mismo número de elementos en el conjunto inicial que en el final.


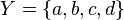




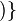








No hay comentarios:
Publicar un comentario