CLASIFICACIÓN DE LAS FUNCION ES DE ACUERDO A LA RELACIÓN ENTRE
DOMINIO Y RANGO

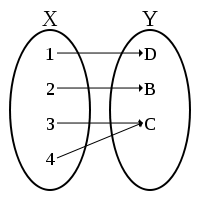
FUNCIÓN INYECTIVA. En esta función a cada elemento del dominio le corresponde
un sólo elemento en el contradominio; es decir, que a argumentos distintos les
corresponden imágenes distintas. A estas funciones también se les conoce como
uno-uno.




Cada número del conjunto A se le asocia solamente con un sólo número en C,
el cual es dos unidades menos.

FUNCIÓN SOBREYECTIVA. En este tipo de funciones el contradominio es imagen;
es decir, todos los elementos del contradominio están relacionados con un elemento
del codominio. En ellas el rango y el contradominio son iguales.
Cada número del conjunto B se asocia con un elemento del conjunto D ( el cual
es el cuadrado del argumento).




FUNCIÓN BIYECTIVA. Este tipo de funciones son tanto uno a uno como sobreyectivas,
también se les llama biunívocas.
A cada elemento del conjunto A se le asocia con uno y sólo un elemento en el
conjunto B (la imagen es el triple del argumento).




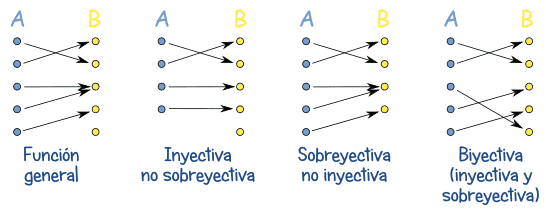
Con darte 3 funciones biyectivas seria suficiente, ya que las 3 serian inyectivas y sobreyectivas, pero para complicar:

f: X->Y

Inyectivas:
X = R+ (reales positivos)
Y = R
f(x) = x + 1
Entonces toda imagen tiene una unica preimagen. O sea y1 = y2 sii x1 = x2.

X = R+
Y = R
f(x) = x^2 + 1

X = R+
Y = R
f(x) = e^x + 1

Sobreyectivas:
X = R
Y = R+
f(x) = |x|
Toda imagen es "alcanzada".

X = R
Y = N
f(x) = e^x

X = R
Y = R+
f(x) = |log(x)|

Y biyectivas pueden ser:

X = R
Y = R
f(x) = x

X = R
Y = R
f(x) = x^3

X = R
Y = R
f(x) = log(x)


Ejemplo: Determinar si la función f :R −→ R tal que f(x) = x + 2 es inyectiva.
Solución
En efecto, sean x1 y x2 dos n´umeros reales cualesquiera, entonces 

                                                                                         f(x1) = f(x2) =⇒ x1 + 2 = x2 + 2 =⇒ x1 = x2      luego f es inyectiva.

Ejemplo: Sea f :A −→ B tal que A = B = R y f(x) = 2x − 3, ∀x ∈ A. ¿Es biyectiva?

Solución
Veamos si es inyectiva y suprayectiva.

(a) Inyectiva. Sean x1 y x2 dos n´umeros reales arbitrarios. Entonces,
f(x1) = f(x2) =⇒ 2x1 − 3 = 2x2 − 3 =⇒ 2x1 = 2x2 =⇒ x1 = x2
luego f es inyectiva.

(b) Suprayectiva. Sea y cualquiera de B. Entonces,

y = 2x − 3 ⇐⇒ 2x = y + 3 ⇐⇒ x = y + 3 /2

luego tomando x = y + 3 / 2, se verifica que x ∈ A y

f(x) = f (y + 3) /2 = (2) ((y + 3) / 2) − 3 = y