Bachillerato VI Semestre

CRITERIO DE LA RECTA VERTICAL

No toda curva es la gráfica de una función, existe una regla geométrica que nos

permite saber si una gráfica es una función o simplemente una relación, este criterio

se enuncia a continuación:

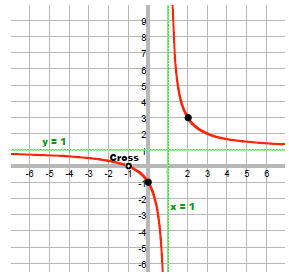
“ Una curva es la gráfica de una función sí y sólo si al trazar rectas

verticales sobre ella, ninguna de ellas la intercepta en más de un

sólo punto a la vez”.

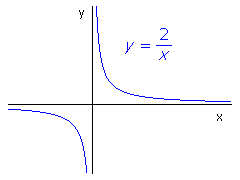
Problemas Resueltos

Ejemplo #1

Encontrar la ecuación de la mediatríz del segmento formado por los puntos A(4,2) y B(-2,10).

$A(4,2)$

$B(-2,10)$

$Distancia PA = Distancia PB$

$\sqrt{(x-4)^{2}+(y-2)^{2}}=\sqrt{(x+2)^{2}+(y-10)^{2}} \:\:\: ()^{2}$

$(x-4)^{2}+(y-2)^{2}=(x+2)^{2}+(y-10)^{2}$

$(x^{2}-8x+16+(y^{2}-4y+4)=(x^{2}+4x+4)+(y^{2}-20y+100)$

Ejemplo #2

Encontrar la ecuación de la recta que pasa por los puntos $(0,0) y (1,k)$

Calculamos la pendiente. $m = \left( \frac{k - 0}{1 - 0} \right)$

$m = k)$

Ahora aplicamos la ecuación de la recta $(y - y_{o})=m(x-x_{o})+b$ sustituyendo los valores que tenemos

$(y - 0)=k(x-0)+b$

$y = kx+b$ tomamos cualquier punto y lo evaluamos para hallar el valor de b

$0= k0+b$

$b = 0$ por lo tanto la ecuación de la recta es

$y = kx$

Ejemplo #3

encuentre la ecuación de la recta que pasa por el punto A( -1, 3) y es paralela a la recta 2y -6x = 10

procedimiento:

$2y -6y = 10$

$2y = 10 + 6x$

$y= \frac{10 + 6x}{2}$

$y = 5 +3x$

$Y = 3x + 5$

luego utilizamos la ecuación general de la recta y llegamos a :

$(y - y_{o})=m(x-x_{o})$

$y - 3 = 3(x + 1)$

$y = 3x + 3 + 3$

la ecuación de la recta que pasa por ese punto es:

$y = 3x + 6$

Pendiente = 3

intersección con el eje Y = (0,6) "hacemos cero a x"

intersección con el eje x = (-2,0) "hacemos cero a y"

Ejemplo #4

Halle la ecuación de la recta que pasa por $(-2,4)$ y es paralela a $x+3y-2=0$ $3y=-x+2$
$y=(-1/3)x+2/3$
utilizamos la ecuación general de la recta :

$(y - y_{o})=m(x-x_{o})$

$(y-4)=(-1/3)x-2/3$
la ecuación de la recta que pasa por ese punto es:

$y=(-1/3)x+10/3$

Ejemplo #5

Halle la ecuación de la recta que pasa por $(-2,5)$ y es perpendicular a $2x+3y-4=0$
$3y=-2x+4$
$y=-\tfrac{2}{3}x+4/3$
utilizamos la ecuacion general de la recta :

$(y - y_{o})=m(x-x_{o})$
la pendiente de una recta perpendicular a ella es el reciproco negativo
$(y-5)=\tfrac{3}{2}x+3$
la ecuacion de la recta que pasa por ese punto es:

$y=\tfrac{3}{2}x+8$

$2y=3x+16$

$2y-3x-16=0$

Ejemplo #6

Encontrar la equacion de la recta que pasa por x el punto P(5,-7) en la recta que es paralela a 6x+3y=4
$6x+3y=4$
$3y=-6x+4$
$y=-2x+4/3$ tenemos que la pendiente es paralela a $m=-2$

$y=mx+b$
$b=y-mx$
$b= -7-(-2(5))$
$b= 3$

Ejemplo #7

Encuentre la ecuacion de la recta que pasa por los puntos (3,2),(4,3)

Primero encontramos el valor de la pendiente:

$m=\frac{\Delta y}{\Delta x}$

Entonces: $m=\frac{3-2}{4-3}= \frac{1}{1}=1$

Ya que tenemos el valor de nuestra pendiente introducimos los valores en la ecuacion de la recta

$(y - y_{o})=m(x-x_{o})$

$y-2=1(x-3)$

$y = x - 3 + 2$

$y = x - 1$

Aca llegamos a nuestra respuesta y podemos ver un grafico de ella

Ejemplo #8

Encuentre la ecuacion de la recta que pasa por los puntos (5,1),(8,3)

Primero encontramos el valor de la pendiente:

$m=\frac{\Delta y}{\Delta x}$

Entonces: $m=\frac{3-1}{8-5}= \frac{2}{3}$

Ya que tenemos el valor de nuestra pendiente introducimos los valores en la ecuacion de la recta

$(y - y_{o})=m(x-x_{o})$

$y-3=\frac{2}{3}(x-8)$

$y -3= \frac{2}{3}x-\frac{16}{3}$

$y = \frac{2}{3}x-\frac{16}{3}+3$

$y = \frac{2}{3}x-2.33$

Aca llegamos a nuestra respuesta y podemos ver un grafico de ella

Ejemplo #9

Encontrar la ecuación de la recta que pasa por los puntos A (1, 3) y B (-2, 1). Determine el intercepto de la recta con el eje y.

Soluciones de Rectas

Ejemplo #10

Del segmento formado por los puntos A(5,2) y B(-2,12), encontrar la mediatriz

$PM\left (\frac{x_2+x_1}{2} ,\frac{y_2+y_1}{2} \right )$

$PM\left (\frac{-2+5}{2} ,\frac{12+2}{2} \right )$

$PM\left (\frac {3}{2} , 7 \right )$

$m= \frac{y_2-y_1}{x_2-x_1}= \frac {10}{-7}$

$m= {-1/-10/7}= \frac {7}{10}$

Forma punto-pendiente de la mediatriz del segmento

$y-y_1 = m (x-x_1)$

Respuesta

$y-7 = \frac {7}{10} (x-\frac {3}{2})$

Lee mas en : La Recta, La Línea Recta, rectas, problemas resueltos - Wikimatematica.org
wikimatematica.org
Follow us: @wikimatematica on Twitter | wikimatematica on Facebook

Bachillerato VI Semestre

martes, 23 de abril de 2013

Problemas Resueltos

Ejemplo #1

Ejemplo #2

Ejemplo #3

Ejemplo #4

Ejemplo #5

Ejemplo #6

Ejemplo #7

Ejemplo #8

Ejemplo #9

Ejemplo #10

No hay comentarios:

Publicar un comentario

Datos personales