FUNCION ESCALONDA:


Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c₁ < c₂ < ... < c_n, y en cada intervalo ]c_k, c_k+1[ es constante, teniendo discontinuidades de salto en los puntos c_k.

Características

Informalmente, una función escalonada es aquella cuya gráfica tiene la forma de una escalera o una serie de escalones (que no necesariamente deben ser crecientes) al ser dibujada. El ejemplo más común de función escalonada es la función parte entera. Otras funciones escalonadas son la función unitaria de Heaviside o función escalón unitario, y lafunción signo.

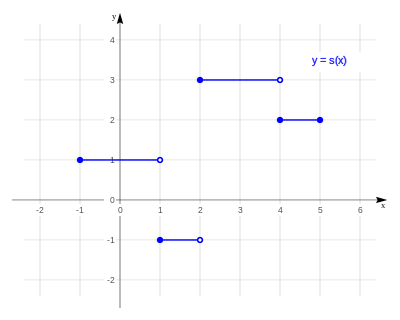
Como caso general podemos ver la función y = s(x), definida así:

En el intervalo cerrado [-1, 5] de números reales sobre los números reales, asociando a cada x de [-1,5] un valor de y, según el siguiente criterio:

Esta función tiene cuatro intervalos escalonados, como se ve en la figura.

La composición de cualquier función escalonada s(x) y una función cualquiera f(x) da por resultado una función escalonada g(x) = f(s(x)), siempre que f(x) esté definida para cualquier valor de x en el rango des(x).

Evidentemente, la derivada de una función escalonada es 0 en cualquier punto en que se halle definida. No puede definirse en los puntos en que hay discontinuidades.

Funciones

1. Aplicaciones de las funciones

En una cuenta de electricidad figura el siguiente detalle:Arriendo de equipos: ............ $ 581
Cargo fijo: .......... $ 492
Energía base 250 KWH........... $ 15.000
Total ........... $ 16.073
El “arriendo de equipos” y el “cargo fijo” suman $1.073 y la “Energía base” se cobra de acuerdo al consumo. En este ejemplo, como cunsumieron 250 KWH (kilowatts-hora), cuyo valor es $15.000, se concluye que cada KWH cuesta: 15.000: 250 = $60.
De lo anterior se deduce que, para calcular el valor de la cuenta, se debe sumar un cargo fijo de $1.073 más $60 por cada KWH de consumo.
Entonces, en términos generales la cuenta C(k) donde k es el número de KWH de consumo, está dada por la expresión:
C(k)=1073+60k
Esta expresión depende de la cantidad “k” (KWH de consumo), por lo que k es la variable independiente y C(k) es la variable dependiente.
En esta notación, C(3) indica el valor de la cuenta para k = 3:
C(3) = 1073 + 60 . 3 = 1253
Es decir, para un consumo de 3 KWH se tiene una cuenta de $1.253.
Esta función la podemos graficar en un plano cartesiano, donde el eje X (eje de las abscisas) corresponde a la variable independiente y en el eje Y (eje de las ordenadas) corresponde a la variable dependiente.
Para graficar la función del ejemplo, construyamos primero una tabla de valores:

Si graficamos estos valores, obtenemos:

Observa que todos los puntos están sobre una recta.
Como veremos más adelante, todas las ecuaciones de la forma: y = mx + n, con m y n constantes reales corresponden a una líneas recta en el plano cartesiano. En este ejemplo: m = 60 y n = 1073.
Una función puede plantear a través de su ecuación, de su gráfica, o bien a través de una situación problemática.
Veamos a continuación cada uno de estos casos:
Ejemplo 1:
Sea la función: f(x) = 3x³-4x²–2x+1. Entonces f(-2) + f(2)=
Solución: Si x = -2, entonces f(-2) = 3.(-2)³–4.(-2)² – 2.(-2)+1=-24 – 16 + 4 + 1= -35
Si x = 2, entonces f(2) = 3.2³-4.2²-2.2+1 = 24 – 16 – 4 + 1= 5
Por lo tanto f(-2) + f(2) = -35 + 5 = -30
Ejemplo 2:
Dada la gráfica de la función mostrada en la figura, hallar el valor de f(-2) + f(2) + f(3):

Solución: Según la gráfica, f(-2) = 2 ; f(2) = -1 y f(3) = -1
Por lo tanto:
f(-2) + f(2) + f(3) = 2 – 1 – 1 = 0
Ejemplo 3:
Una piscina es llenada por una manguera en forma constante de modo que la altura alcanzada por el agua aumenta 20 cm por cada hora que transcurre.
Si inicialmente el agua que había en la piscina llegaba a una altura de 1,2 m, ¿cuál es la ecuación de la función que determina la altura (h) del agua después de transcurridas t horas?
Por cada hora que transcurre la altura crece en 0,2 m, por lo tanto, la altura que aumenta el agua después de t horas es: 0,2t.
Así, la altura h después de t horas, está dada por la relación: h(t) = 1,2 + 0,2t
Puedes hallar ejercicios y aplicaciones de funciones en el sitio:
Función afín
2. Fórmulas de Geometría Analítica
A continuación veremos algunas fórmulas básicas de la geometría en el plano cartesiano.Dados los puntos A, de coordenadas (x₁,y₁) y B, de cooredenadas (x₂,y₂), entonces:
i. Distancia entre A y B : 
ii. Coordenadas del punto medio del segmento : 
iii. Pendiente del segmento : 
iv. Ecuación principal de la recta: x es la variable independiente, y es la variable dependiente, m es la pendiente de la recta y n es el coeficiente de posición.
v. Ecuación general de la recta: ax + by + c = 0 ; a, b y c son constantes reales, x e y son las variables
3. Función lineal
Una función lineal es de la forma: f(x) = mx + n , y su gráfica es una línea recta en el plano cartesiano. Si f(X) = Y , entonces la función lineal se escribe y = mx + n, lo que corresponde a la ecuación principal de una recta, definida en el número iv anterior.
La pendiente de la recta es m y su signo está relacionado con el ángulo que forma ella con el eje X (medido en sentido contrario a los punteros del reloj).
Interpretación del signo m:
Si la pendiente es positiva, la recta forma un ángulo agudo con el eje X.

Si la pendiente es negativa, la recta forma un ángulo obtuso con el eje X.

Interpretación geométrica del coeficiente de posición n.
geométricamente, el coeficiente de posición se denomina n indica la intersección de la recta con el eje Y o eje de las ordenadas, es decir, en toda ecuación de la forma: y = mx + n, su gráfica intercepta al eje Y en el punto de coordenadas (0,n).Veamos a continuación algunos ejemplos de interpretación de m y n:

4. Rectas paralelas y perpendicularesSi tenemos las pendientes de dos rectas, entonces podemos determinar si son paralelas o perpendiculares, a través de las siguientes propiedades:

• Si dos rectas son paralelas entonces tienen igual pendiente.
• Si dos rectas son perpendiculares entonces el producto de sus pendientes es –1.

Ejemplo 1:
Dadas las rectas: L₁: 5x – 3y = 15 y L₂: 3x + 5y = 12, determina si son paralelas o perpendiculares.
Solución: Primero se debe convertir cada recta a su ecuación principal, despejando la variable y:

La pendiente m corresponde al coeficiente de la variable x, por lo tanto:

Multiplicando ambas pendientes obtenemos:

Y, por lo tanto las rectas son perpendiculares.

Ejemplo 2:
¿Cuál es el gráfico de la función 3x-2y+6=0?
Solución: Primero llevamos la ecuación general a la ecuación principal:

de esta última ecuación concluimos que m = y n = 3, por lo tanto su gráfica aproximadamente es:

Ejemplo 3:
¿Cuál es el valor de p si el punto (2p-1,p+1) pertenece a la recta 3x-2y+1=0?
Solución: Reemplazamos las coordenadas (x, y) del punto en las respectivas variables de la ecuación de la recta:
x = 2p - 1 ; y = p + 1
3(2p – 1) –2(p + 1) + 1 = 0
4p –4 = 0 p = 1
Ejemplo 4:
¿En qué punto la recta de ecuación: 3x – 2y + 9 = 0 corta el eje X?
Soñución: El punto donde la recta intercepte al eje x debe tener su coordenada y igual a cero, luego reemplazamos y = 0 en la ecuación de la recta:
3x – 2 . 0 + 9 = 0 
Por lo tanto intercepta al eje x en el punto (-3, 0).
Se recomienda visitar los siguientes sitios para trabajar la función lineal y aspectos relativos a ella:
En la siguiente dirección de Internet se puede trabajar con un graficador de funciones lineales y afines. Permite observar cómo se comporta el gráfico de la recta de ecuación: y = mx+k, al modificar los valores de los parámetros m y k.
Función lineal afín
- Doce ejercicios de aplicación de la función lineal:
http://www.atodahoratuclase.com.ar/polinomios.doc
- Ocho ejercicios de ecuaciones de rectas: (no considerar el 9º que corresponde a sistemas de ecuaciones)
http://www.cam.educaciondigital.net/pbs1/mate1pbs/Trabajo%20Practico%20Funciones%20Lineales.doc
FUNCIÓN VALOR ABSOLUTO
Se define la función valor absoluto o módulo como , donde . Debes recordar que la expresión -x no representa necesariamente a un número negativo, sino que representa al opuesto o inverso aditivo de x, es decir, si x = 4, -x =-4, pero si x = -7, entonces -x = -(- 7) = 7.
Para esbozar el gráfico de esta función podemos construir una tabla de valores con una cantidad suficiente de puntos y luego situamos dichos puntos en un sistema de ejes coordenados.
 
Observando el gráfico anterior, concluimos que:
i) El dominio de esta función es el conjunto ℝ (los números reales) y su recorrido es el conjunto ℝ+ ∪ { 0 } (los reales positivos con el cero),
ii) Tiene su vértice en el punto (0, 0).
iii) Sus ramas se abren hacia arriba.
iv) Tiene por eje de simetría a la recta de ecuación x = 0.
Veamos un par de variaciones de la función valor absoluto.
Ejemplo 1. ¿Cuál es el gráfico de la función f(x) = | x – 2 |?
Solución. Nuevamente construimos una tabla de valores.
 
Observando el gráfico concluimos que:
i) El dominio de esta función es el conjunto ℝ (los números reales) y su recorrido es el conjunto ℝ+ ∪ { 0 } (los reales positivos con el cero).
ii) Tiene su vértice en el punto (2, 0).
iii) Sus ramas se abren hacia arriba.
iv) Tiene por eje de simetría a la recta de ecuación x = 2.
Ejemplo 2. ¿Cuál es el gráfico de la función f(x) = | x | – 2?
Solución. Construyendo la tabla de valores, tenemos:
 
Observando el gráfico anterior, concluimos que:
i) El dominio de esta función es el conjunto ℝ (los números reales) y su recorrido es el conjunto [-2, ∞[.
ii) Tiene su vértice en el punto (0, 0).
iii) Sus ramas se abren hacia arriba.
iv) Tiene por eje de simetría a la recta de ecuación x = 0.
Ejemplo 3. ¿Cuál es el gráfico de la función f(x) = 2 - | x |?
Solución. Construyendo la tabla de valores, tenemos:
 
Observando el gráfico anterior, concluimos que:
i) El dominio de esta función es el conjunto ℝ (los números reales) y su recorrido es el conjunto ]-∞, 2].
ii) Tiene su vértice en el punto (0, 2).
iii) Sus ramas se abren hacia abajo.
iv) Tiene por eje de simetría a la recta de ecuación x = 0.
FUNCIÓN PARTE ENTERA
Se define la parte entera de un número real x como [ x ] = El mayor entero menor o igual que x. Para comprender esta definición, veamos algunos ejemplos.
Ejemplo 1. Para calcular la parte entera de 4, de acuerdo a la definición, debemos pensar en todos los enteros menores o iguales que 4, o sea, se trata del conjunto:
{-∞, … , -5, -4, -3, -2, -1, 0, 1, 2, 3, 4}
Ahora, nos quedamos con el mayor de estos enteros, el 4. Por lo tanto, [ 4 ] = 4.
Ejemplo 2. Calcular [ -2 ]. El conjunto de los enteros menores o iguales que -2 es:
{-∞, … , -6, -5, -4, -3, -2}
El mayor número de este conjunto es -2, por lo tanto, [ -2 ] = -2.
Ejemplo 3. Calcular [ 1,763 ]. El conjunto de los enteros menores o iguales que 1,763 es:
{-∞, … , -5, -4, -3, -2, -1, 0, 1}
Y el mayor de estos números es 1, por lo tanto, [ 1,763 ] = 1. Es decir, cuando calculamos la parte entera de un número decimal positivo, nos quedamos con la cifra que se encuentra delante de la coma decimal.
Ejemplo 4. Calcular []. El conjunto de los enteros menores o iguales que es:
{-∞, … , -5, -4, -3, -2, -1, 0, 1, 2}
por lo tanto, [] = 2.
Ejemplo 5. Calcular [ -2,7 ]. El conjunto de los enteros menores o iguales que -2,7 es:
{-∞, … , -6, -5, -4, -3}
por lo tanto, [ -2,7 ] = -3. Luego, cuando calculamos la parte entera de un número decimal negativo, a la cifra que se encuentra delante de la coma se le resta 1.
Ejemplo 6. Calcular [ -p ]. El conjunto de los enteros menores o iguales que -p (-p ≈ -3,14) es:
{-∞, … , -6, -5, -4}
entonces, [ -p ] = -4.
Se define la función parte entera de x como f(x) = [ x ]. Para esbozar su gráfico, nos construimos una tabla de valores y luego trasladamos los puntos al gráfico.

Ejemplo 1. Calcular: 
Solución. 
Ejemplo 2. Calcular: 
Solución. 
Ejemplo 3. Determinar el gráfico de la función f(x) = [ x ] + 1.
Solución. Después de construir una tabla de valores adecuada, el gráfico resultante es:

Ejemplo 4. En un almacén venden dulces a $50 la unidad. ¿Cuál es la función que representa la cantidad “y” de dulces que se pueden comprar con $ x (x Î ℝ+ ∪ {0})?
Solución. Con $ 0 y con cualquier cantidad menor a $ 50 se pueden comprar 0 dulces. Si se tiene cualquier cantidad mayor o igual a $ 50 y menor que $ 100, sólo se puede comprar 1 dulce. Con cualquier cantidad mayor o igual a $ 100 y menor que $ 150 se pueden comprar 2 dulces, y así sucesivamente. Por lo tanto, la función buscada tiene la forma de la función parte entera con los parámetros convenientemente adaptados.

Y su forma analítica será: