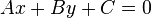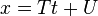Una ecuación de primer grado o ecuación lineal significa que es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia.

Formas complejas como las anteriores pueden reescribirse usando las reglas del álgebra elemental en formas más simples. Las letras mayúsculas representan constantes, mientras x e y son variables.
Ecuación general
-
- Aquí A y B no son ambos cero. Representa una línea en el cartesiano. Es posible encontrar los valores donde x e y se anulan.
- Ecuación segmentaria o simétrica
-
- Aquí ni E ni F no pueden ser cero. El gráfico de esta ecuación corta al eje X y al eje Y en E y F respectivamente.
- Forma paramétrica
- Dos ecuaciones que deben cumplirse de manera simultanea, cada una en la variable t. Puede convertirse a la forma general despejando t en ambas ecuaciones e igualando.
- Casos especiales:
- Un caso especial es la forma estándar donde
 y
y  . El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con ese eje.
. El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con ese eje.
- Otro caso especial de la forma general donde
 y
y  . El gráfico es una línea vertical, interceptando el eje X en E.
. El gráfico es una línea vertical, interceptando el eje X en E.
- En este caso, todas las variables fueron canceladas, dejando una ecuación que es verdadera en todos los casos. La forma original (no una tan trivial como la del ejemplo), es llamada identidad. El gráfico es todo el plano cartesiano, ya que lo satisface todo par de números reales x e y.
Nótese que si la manipulación algebraica lleva a una ecuación como 1 = 0 entonces la original es llamada inconsistente, o sea que no se cumple para ningún par de números x e y. Un ejemplo podría ser: 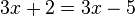 .
.
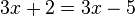 .
.
Adicionalmente podría haber más de dos variables, en ecuaciones simultaneas. Para más información véa: Sistema lineal de ecuaciones
Las funciones de segundo
Las funciones de segundo grado o parabólicas tienen mucho uso dentro del mundo de los videojuegos, piensa en Super Mario o en cualquier juego de plataformas 2D que hayas jugado. Cuando saltas el movimiento que describe el personaje es un movimiento parabólico que se puede obtener con una función de segundo grado. Tienen el siguiente aspecto.
Para dibujar su gráfica podríamos usar el método de ir dándole valores a la x y obtener sus respectivas y, pero necesitaríamos muchos puntos para poder dibujar bien, lo mejor es buscar los puntos claves. Los puntos de corte con los ejes y el vértice.
Ecuación de tercer grado
Una ecuación de tercer grado o ecuación cúbica con una incógnita es una ecuación que se puede poner bajo la forma canónica:
- ,
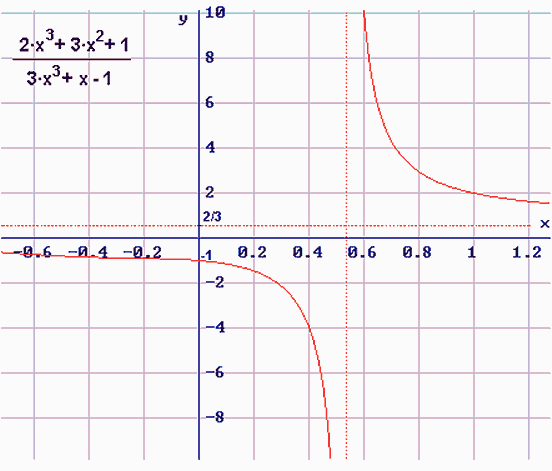
La función cúbica
Es una función polinómica de tercer grado. Tiene la forma:
donde el coeficiente a es distinto de 0.
Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.
La derivada de una función cúbica genera una función cuadrática y su integral una función cuártica.
Discriminante
Resulta importante y a la vez esencial obtener propiedades elementales de los polinomios como herramientas de análisis en los resultados según los valores de sus coeficientes. Cualquier ecuación cúbica con coeficientes reales tiene al menos una solución x sobre los números reales; esta es una consecuencia del teorema del valor intermedio. Se pueden distinguir varios posibles casos, usando para ello el discriminante.
Los siguientes casos necesitan ser considerados:
- Si Δ > 0, entonces la ecuación tiene tres distintas raíces reales.
- Si Δ = 0, entonces la ecuación tiene múltiples raíces y todas sus raíces son reales (puede ser una raíz triple o una doble y otra simple).
- Si Δ < 0, Entonces la ecuación tiene una raíz real y dos raíces complejas conjugadas.
FUNCION CUARTICA
 ) son números que pertenecen a un cuerpo, usualmente a los reales
) son números que pertenecen a un cuerpo, usualmente a los reales  o los complejos
o los complejos  .
.
El método siguiente permite obtener las cuatro raíces al mismo tiempo. Este método es llamado "método de Descartes"
Método de Descartes
Los pasos de la resolución para el método de Descartes son:
- Dividir la ecuación inicial por el coeficiente a
- Proceder al cambio de incógnita para suprimir el término cúbico. ras sustituir x y operando con las identidades notables,
- Y ahora, la idea genial: factorizar lo anterior
- Desarrollando la expresión e identificando los dos polinomios, obtenemos las condiciones:
- Después de algunos cálculos y lo hallamos es una ecuación de tercer grado en la variabley que se puede resolver usando el método de Cardano.
y=5x^4